1. Introduction Machine Learning for Graphs

1. Introduction: Machine Learning for Graphs

所有笔记参照于slide。

1. 无向图和有向图——有无方向(有无箭头)

2. 各种各样的图

图的表示$G = (V, E, R, T)$.其中：

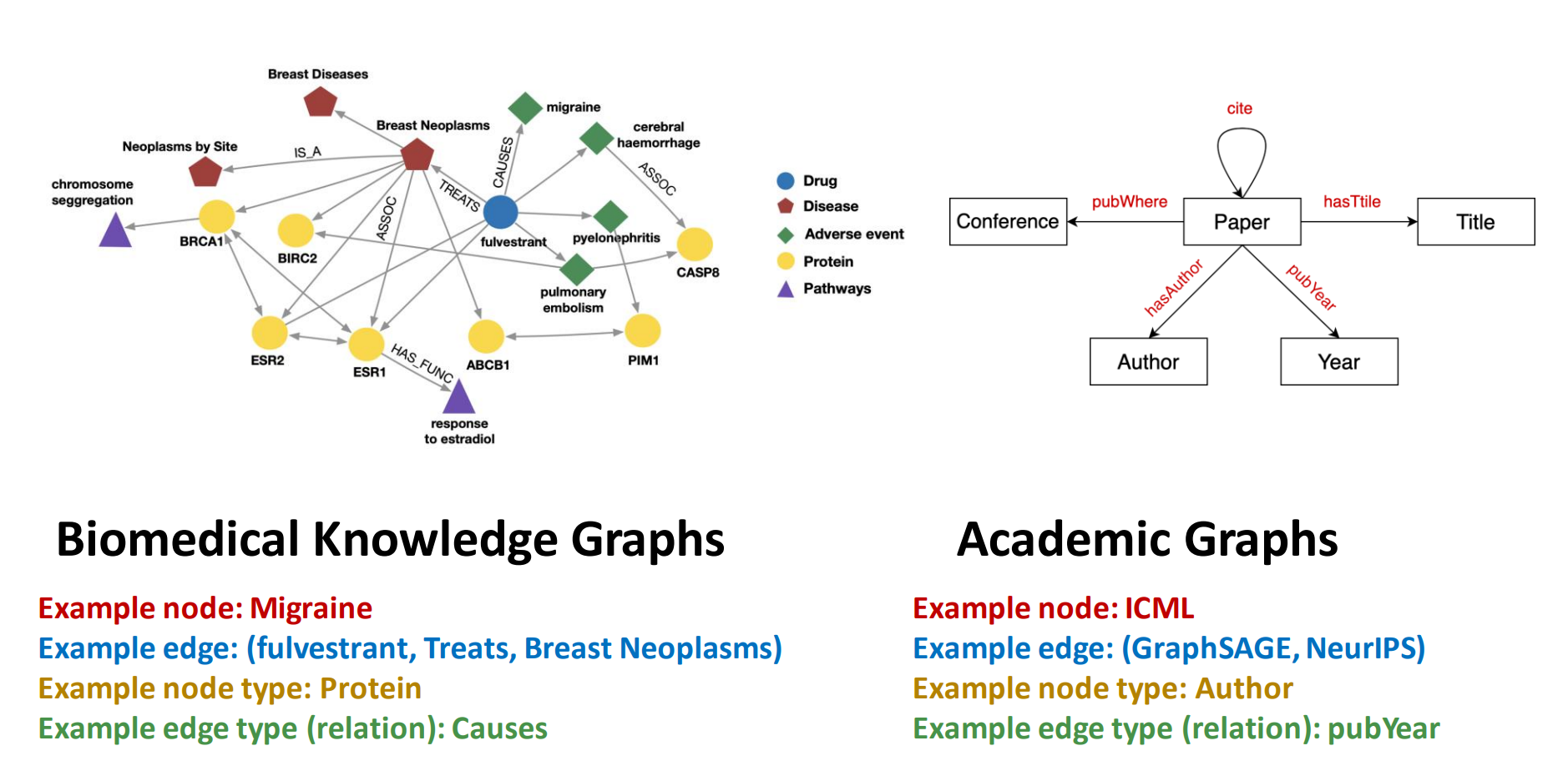
1. V：节点的集合$v_i \in V$.
2. E: 表示节点间关系$(v_i, r, v_j) \in E$，即这个三元组构成边，或者说边表示了这三者关系
3. $T(v_I)$: 节点类型
4. 关系类型$r \in R$

下面这两个例子就很清楚绘制了图网络是怎么表示各种节点、节点类型以及边代表的关系。如Causes, pub Year.

3. 节点的度

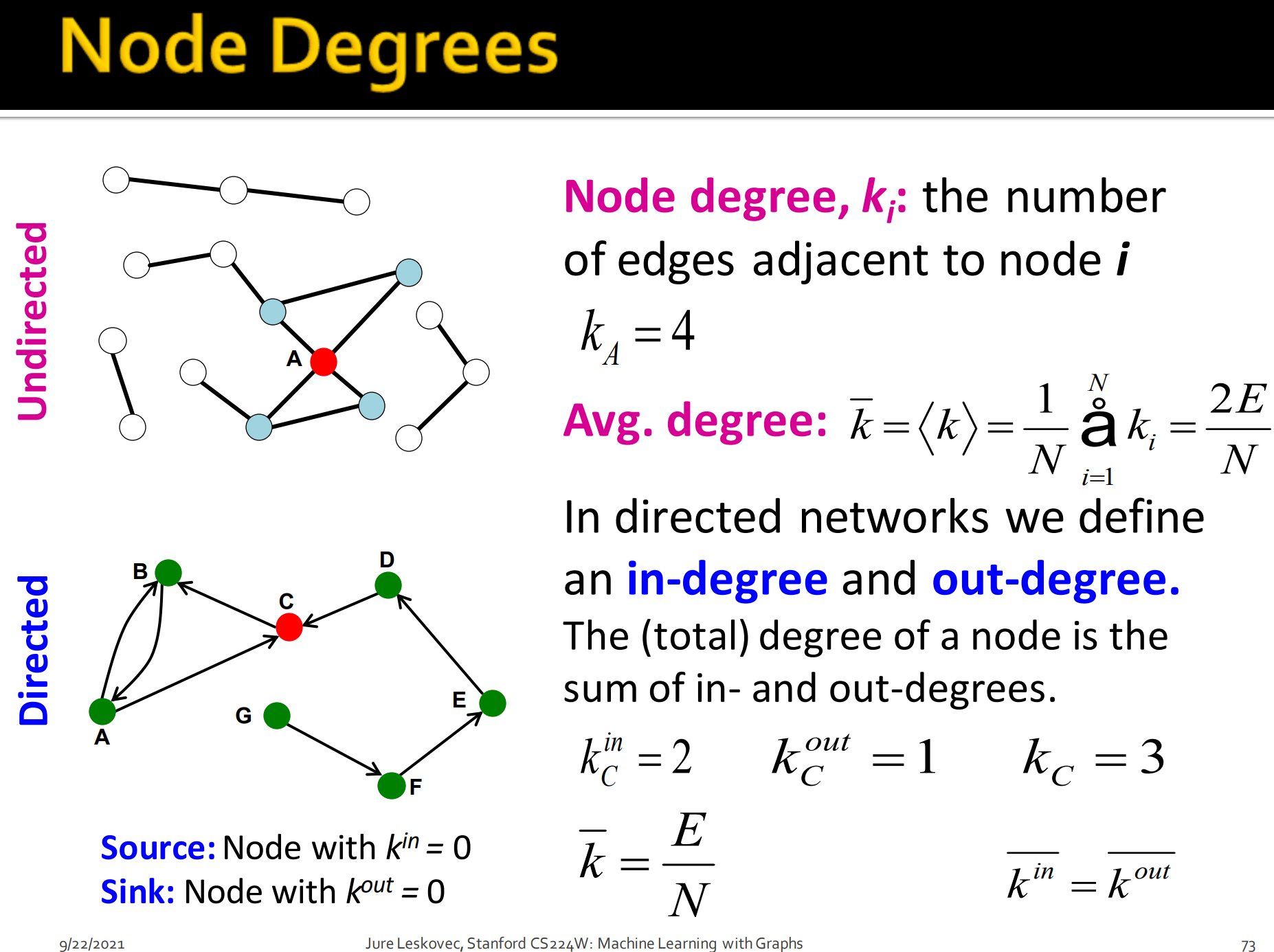
1. 无向图: 直接看该节点的连接边数目，如上图中，A的度就是4. 平均的度等于所有节点的度的平均值，也等于边数的2倍除以节点数$\frac{2E}{N}$。
2. 有向图:
   • 对于节点:分为出度和入度，就看箭头指向，指向该节点是入度，从该节点出发是出度。上图中C的入度是2，出度是1.度为3。
   • 对于图: 有向图平均度为$\frac{E}{N}$,并且对于整个图来说，平均出度和入度应该相等。其用来: 衡量图的稠密性

注:

• Source: 节点的入度为0，就没有箭头指向该节点，(万物源于此)，这种节点叫做起始点。
• Sink: 节点的出度为0，该节点没有箭头出来，终止了，这种节点叫做终止点。
• 总结:起始点（Source Node）入度为0、终止点（Sink Node）出度为0。

4. 二分图

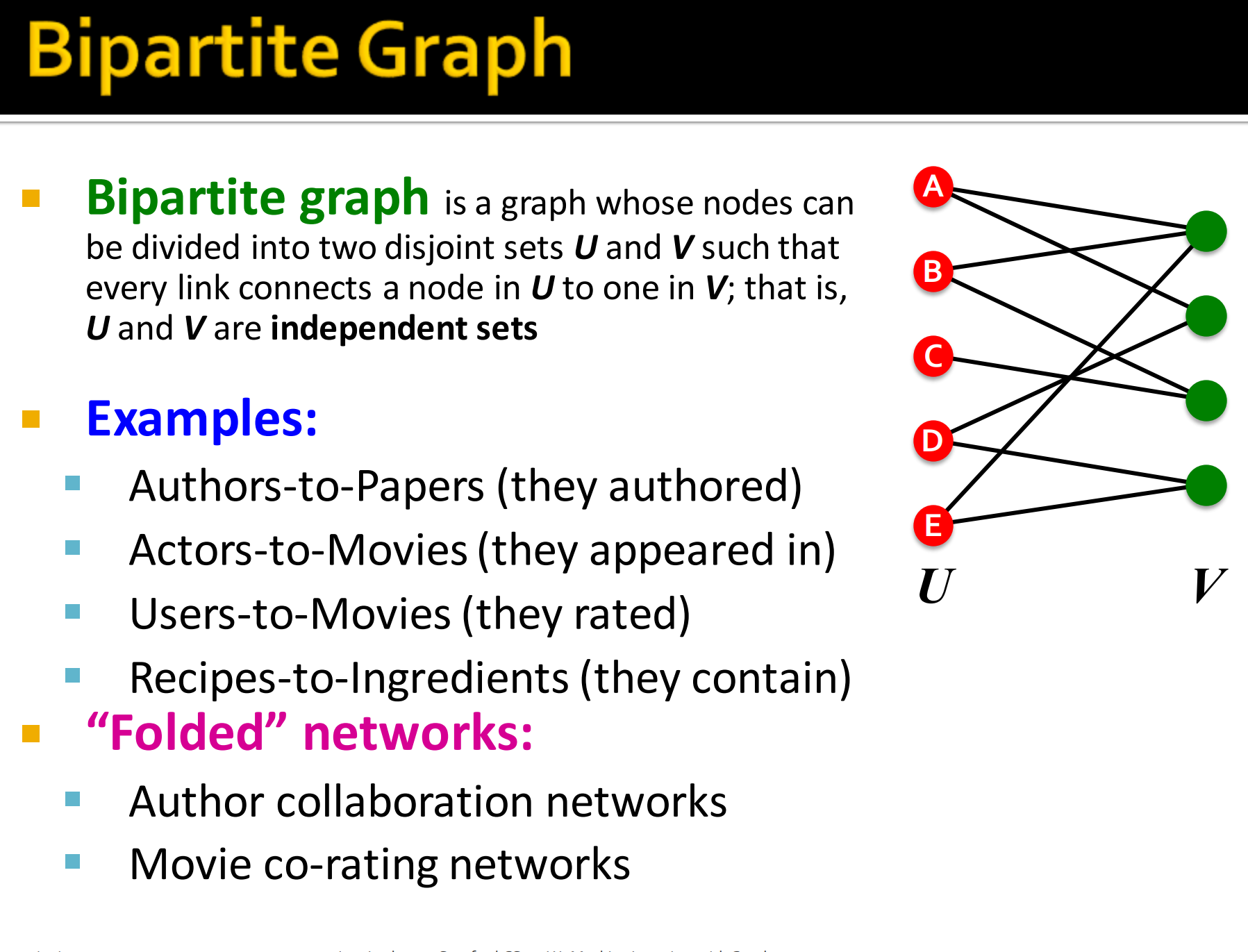
二分图是一种内部节点可分为没有交集的集合U和集合V，使得每个边都连接一个U中的节点和集合V的节点。这样U和V都是独立的集合。(如上图，集合U中的节点是没有边的，集合V中的节点也是没有边的，这样的集合就是独立的)。

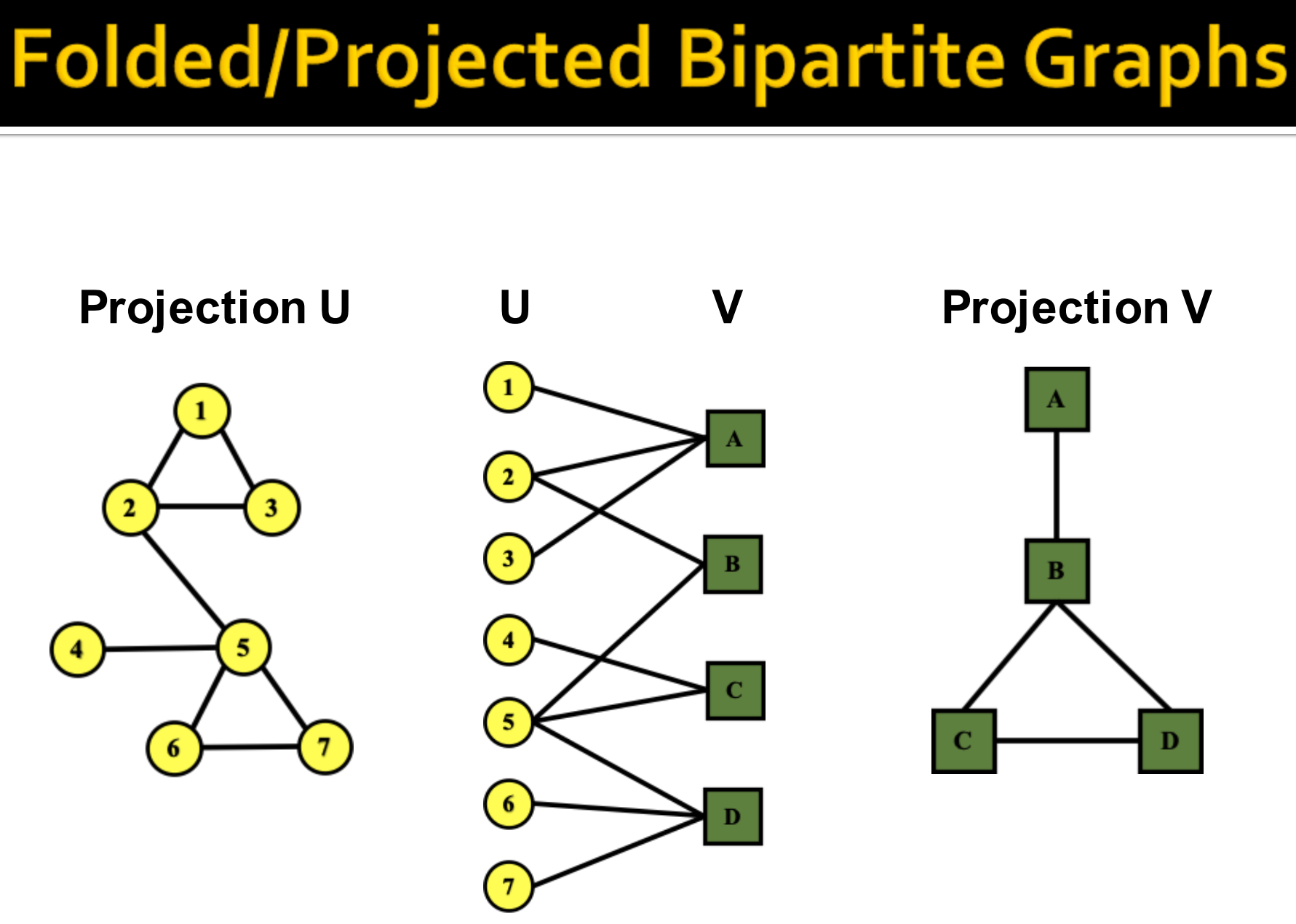
折叠和投影二分图

如果集合U和集合V共享至少一个共同的邻居，就可以通过在独立集合中创建边来折叠(Folded)二分图。如下图，集合U中的节点至少共享一个集合V中的邻居节点，集合U中的节点连接形成投影U，同样获得投影V。

5. 邻接矩阵

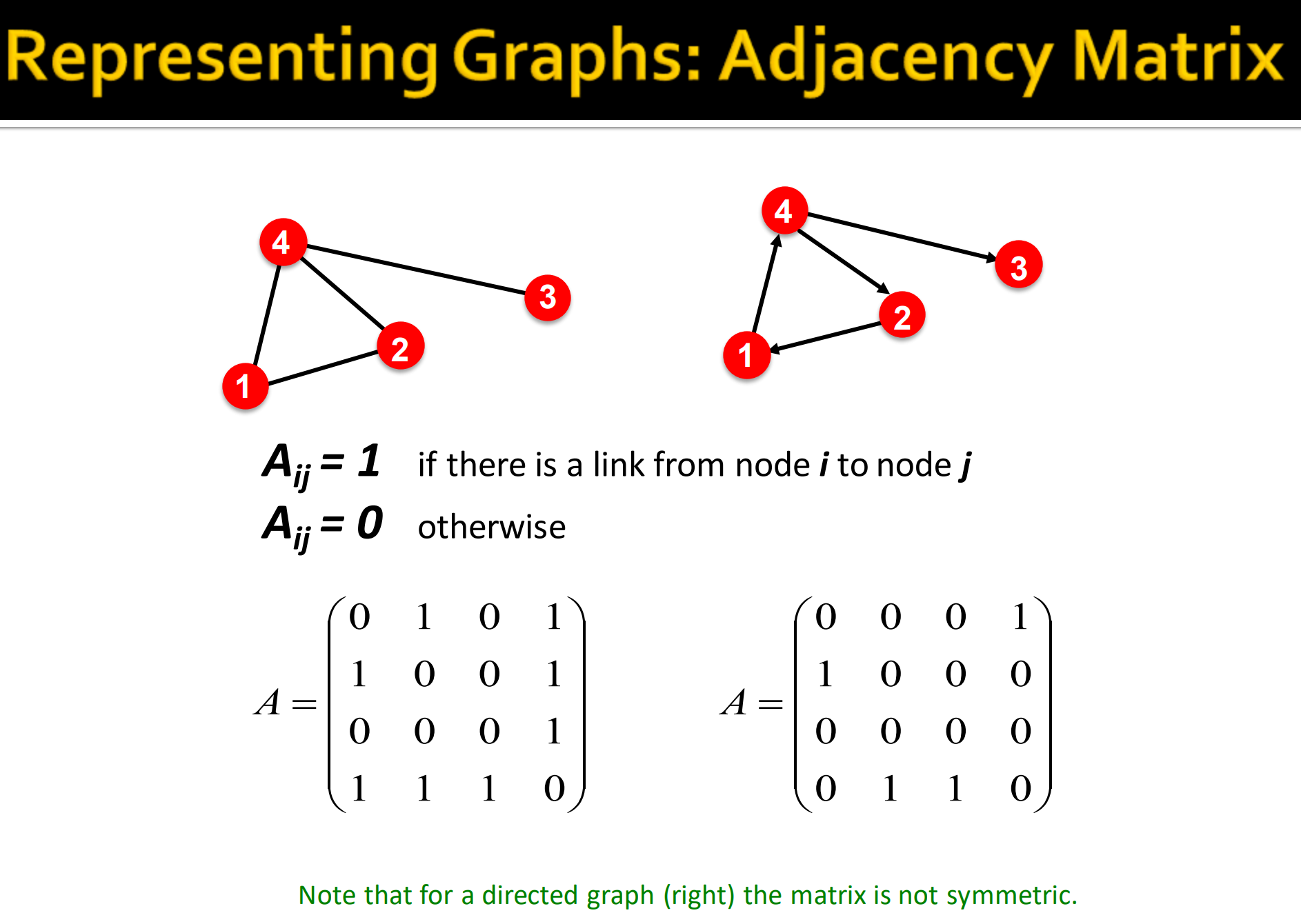
就是拿一个矩阵来表示图中每个节点的连接关系。

其中，$A_{ij}=1$ 表示从节点i到节点j有节点相连，而等于0就是不相连。

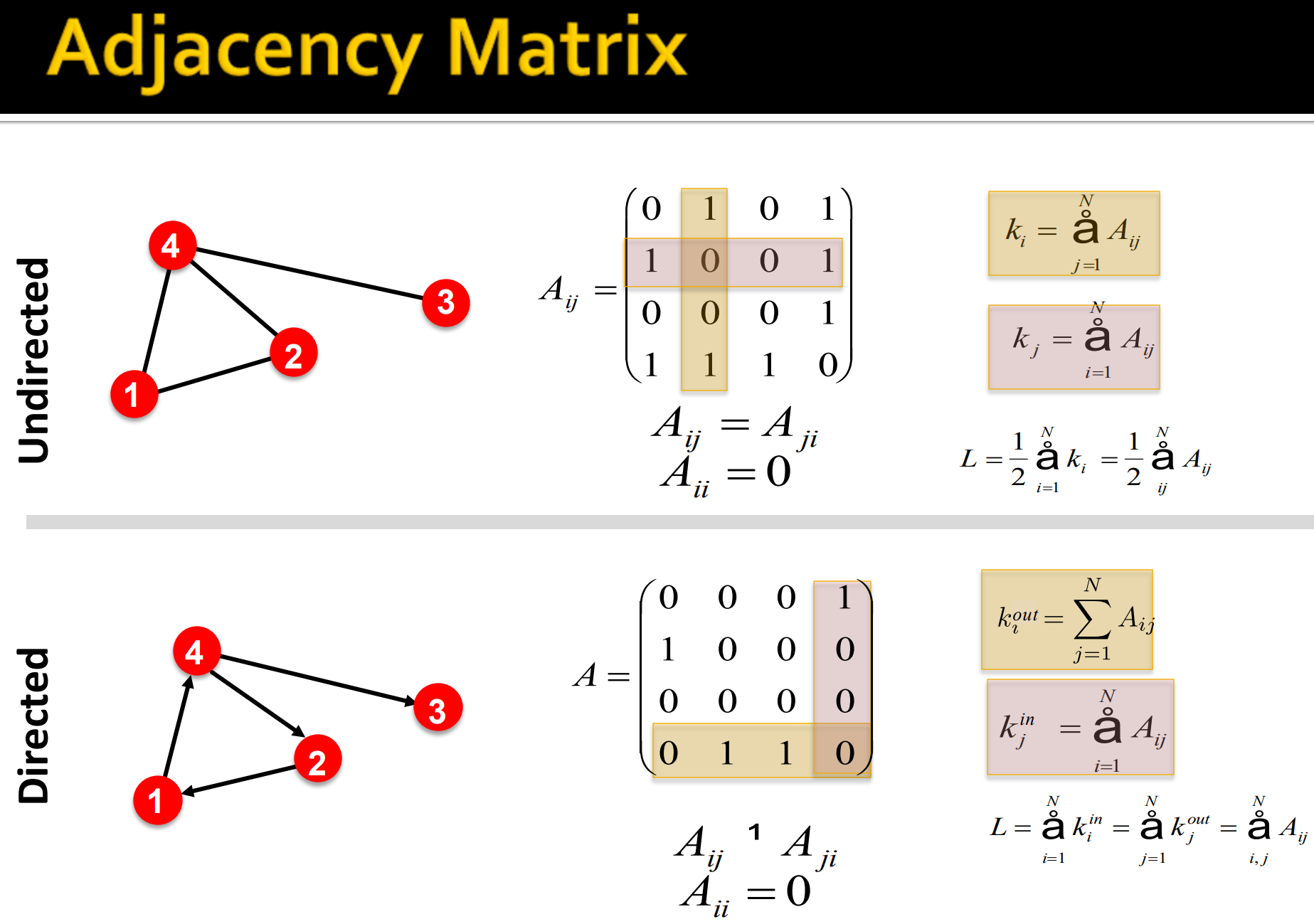
1. 无向图: $A_{ij} = A_{ji}, \ A_{ii}=0$，无向图的邻接矩阵是一个对称矩阵。
2. 有向图:非对称矩阵。

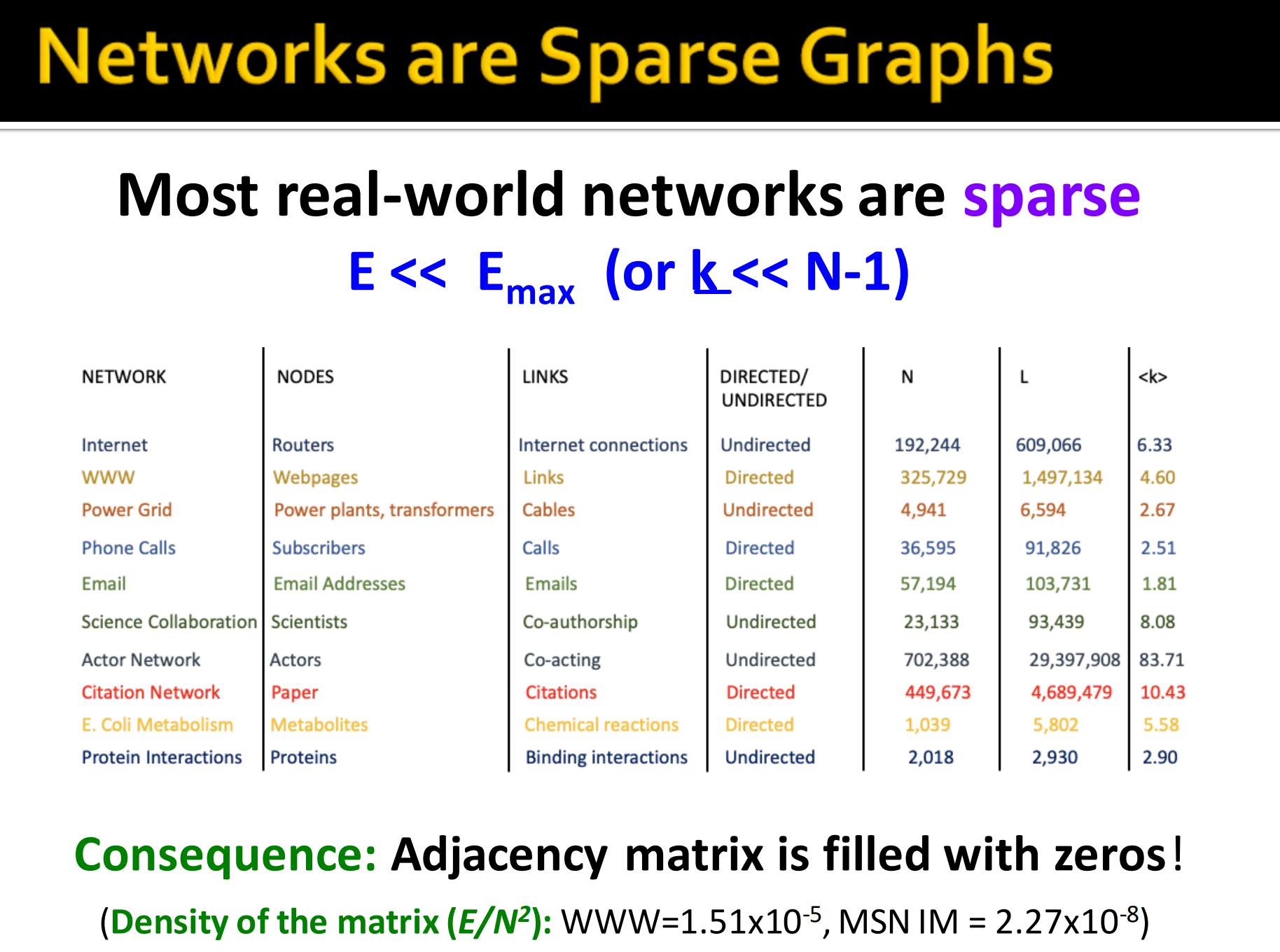
绝大多数情况下，邻接矩阵是稀疏的。( $|E| \ll E_{m a x} \ \text{or } \bar{k} \ll N-1$)。结果导致邻接矩阵被大量的零填充(不期望的属性)。

为了缓解此问题，我们可以将图形表示为一组边(边链表)。这虽然使边缘查找更加困难，但是节省了内存。

6. 图表示： 边列表

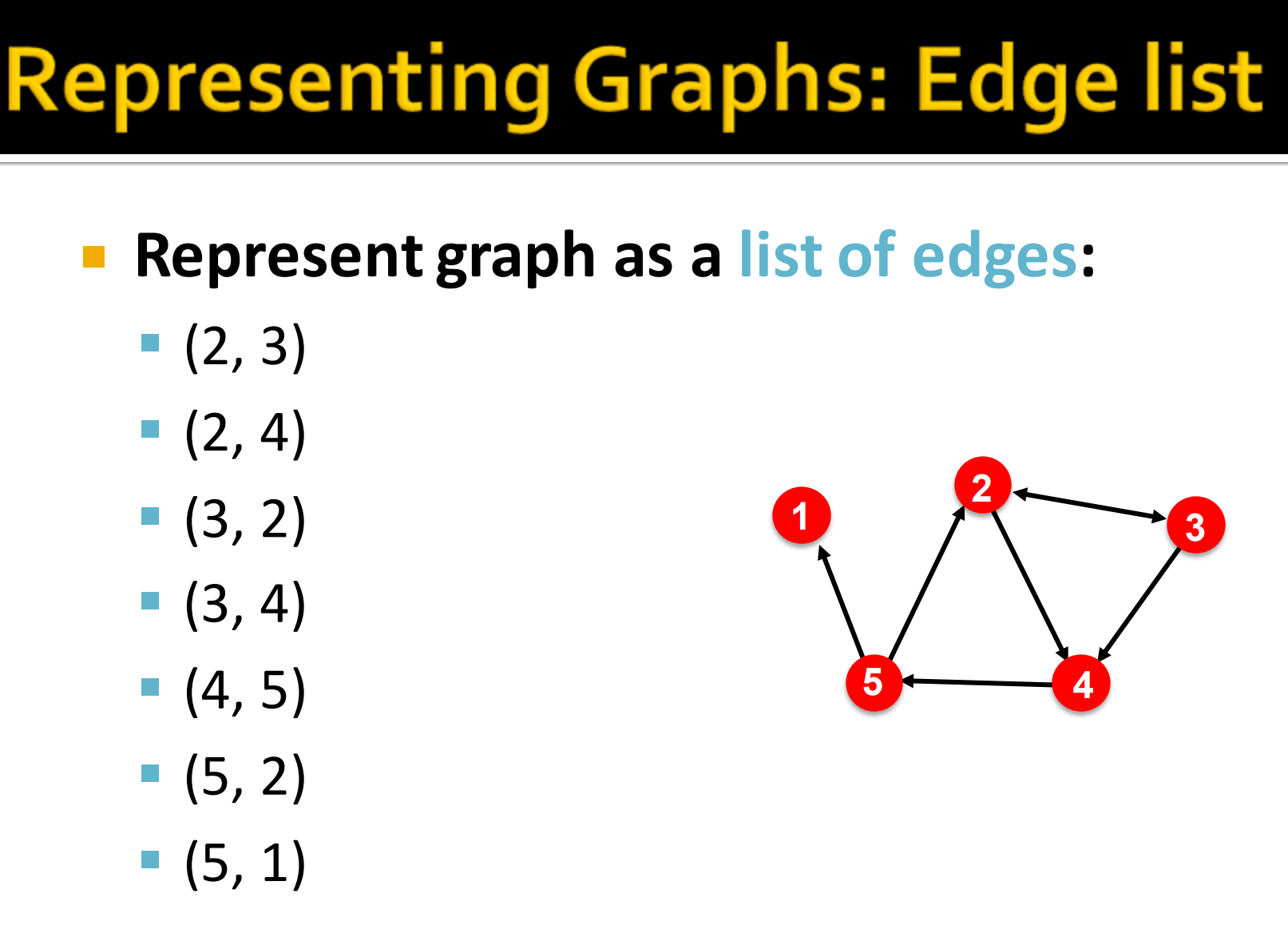
就把连接关系拿一个元组表示，再组成一个列表(字典)。

7. 权重图——边是有权重的

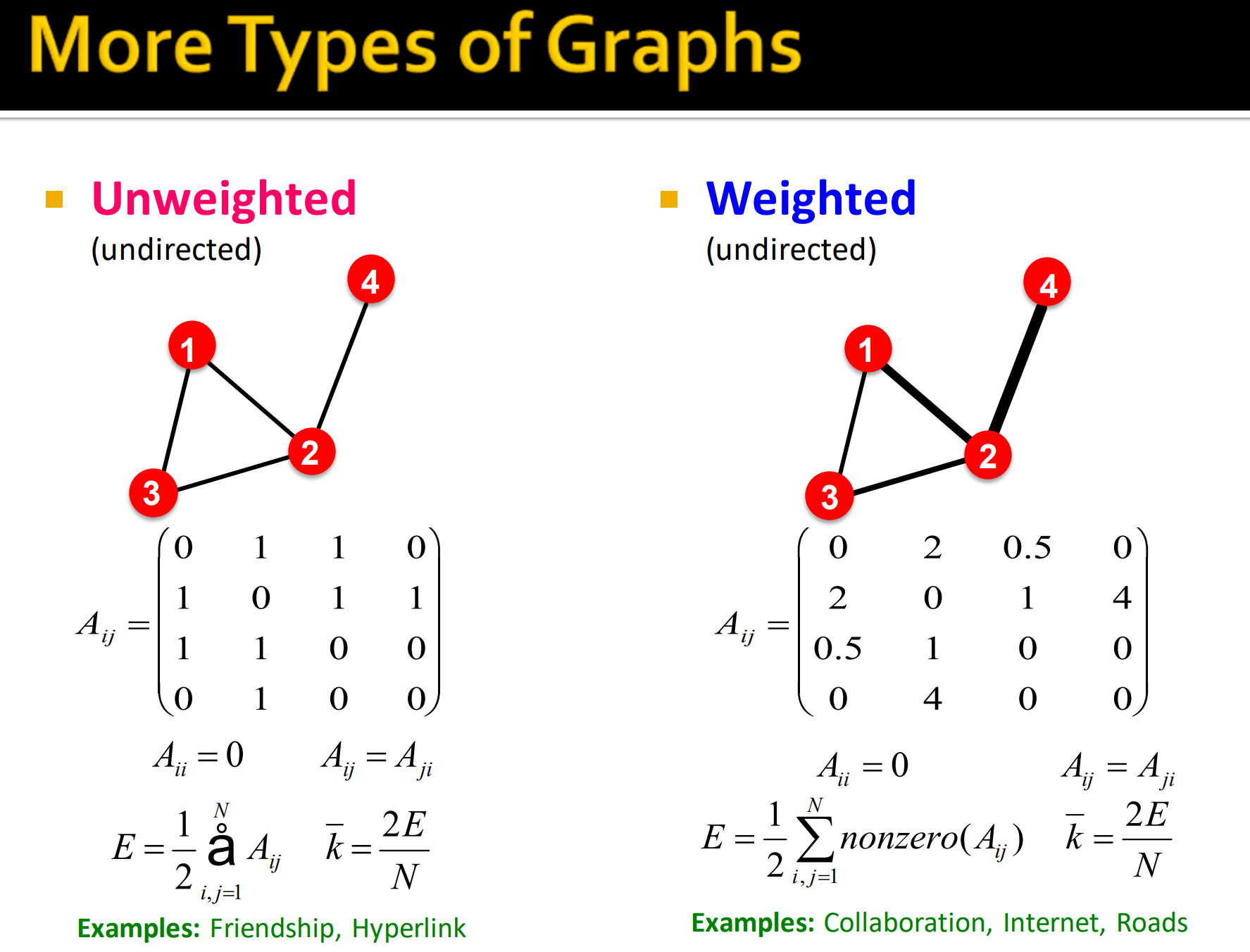
8. 自循环和多图

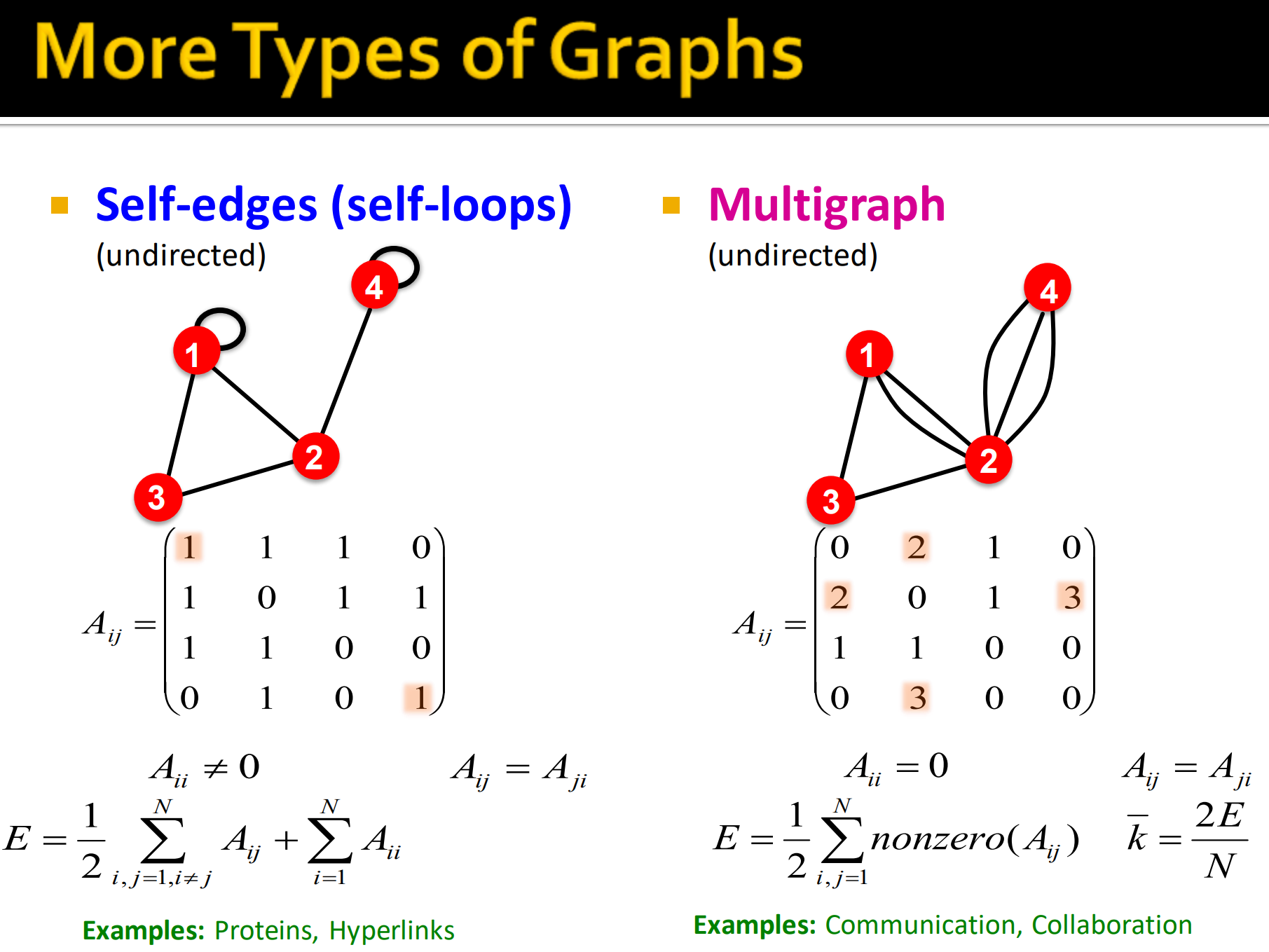
1. 完全图（complete graph）: 任意两点都有边相连。
2. 自环图（Self-edges (self-loops)）: 自己与自己相连，邻居矩阵的对角线不为0.
3. 多重图 （ Multigraph ）: 存在两点之间大于一条边。

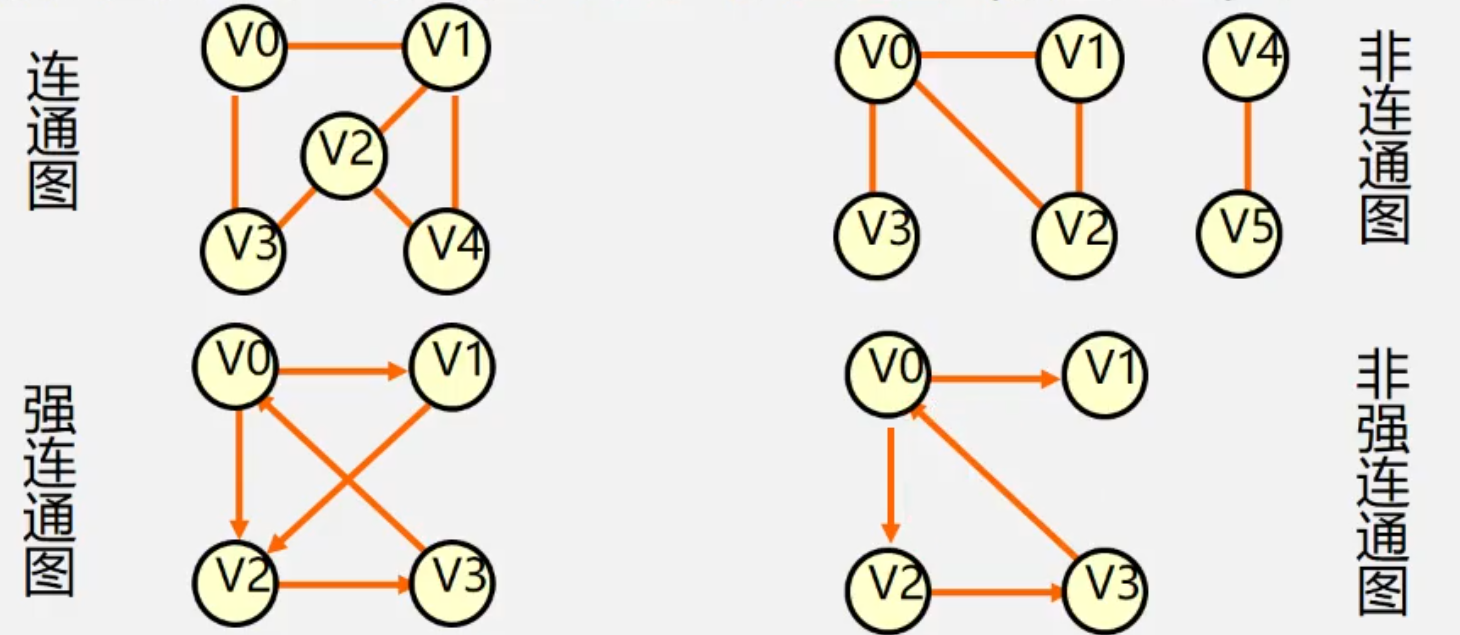
9. 无向图的连通性

任意两节点存在直接或间接的连接关系，就认为其是连通的。Bride edge(桥边)是指删除后能使图变成非连通图的边。

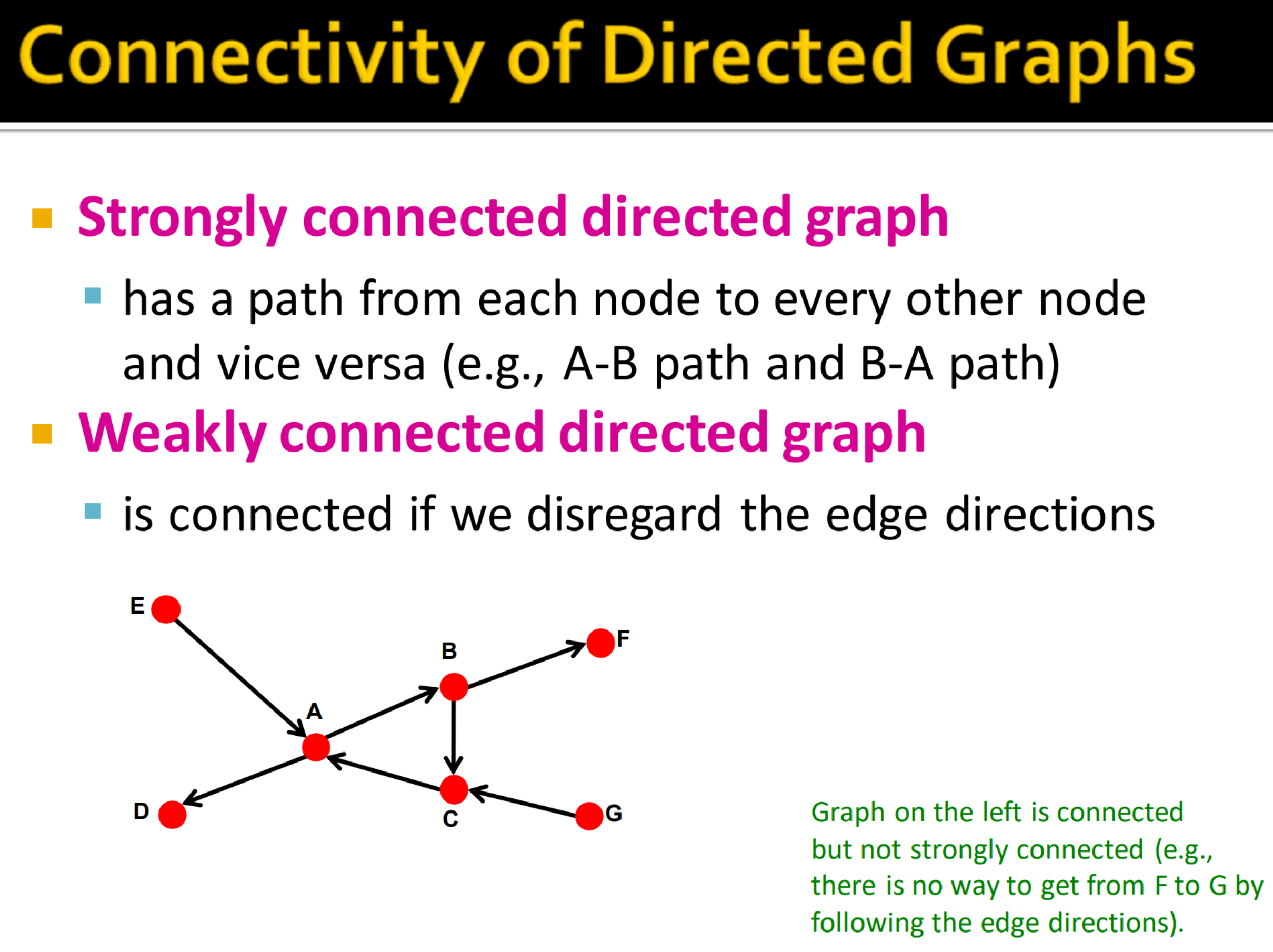
10. 有向图的连通性

1. 强连通: 对于两个任意节点，存在来回路径，两个节点互相都能到达。
2. 弱连通: 忽略方向是才连通的。

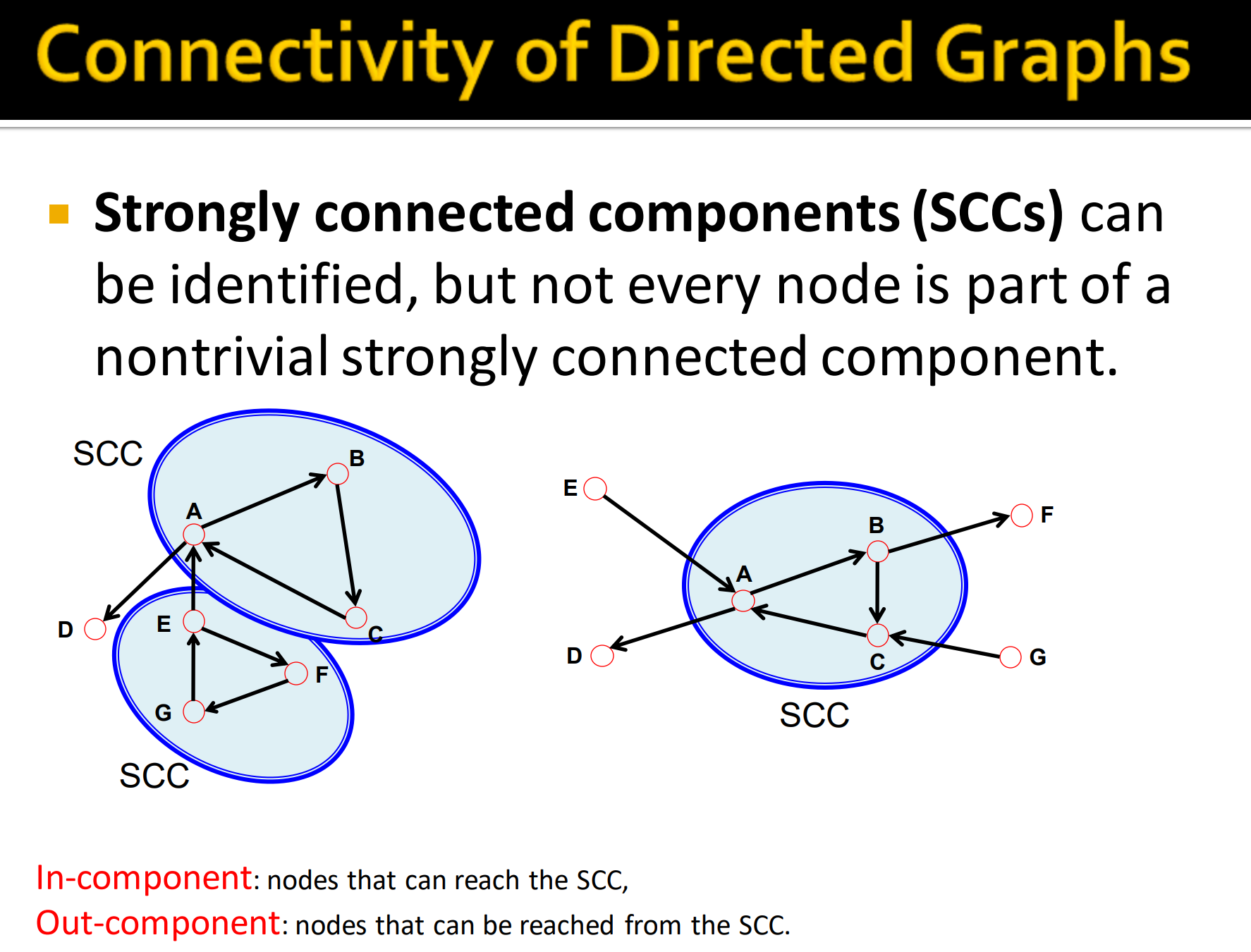
强连通分量 SGCs:可以看作是一组节点组成了强连通。如$G[A, B, C]$就形成了一个SGC，$G[E, F, G]$也一样。

数据结构里面关于图的知识点，可以跳过。

图：$G=（V,E）\Longrightarrow \text{Graph} = (\text{Vertex}, \text{Edge})$

其中，

• V是顶点(数据元素)的有穷非空集合；

• E是边的又穷集合。

• 无向图：每条边都是无方向的

• 有向图：每条边都是有方向的。

• 完全图：图中的任意两个点都有一条边相连。

  ​ 对于n个顶点，

  ​ 无向完全图有$n(n-1)/2$条边，有向完全图有$2C_n^2 = n(n-1)$.

• 稀疏图：有很少边或弧的图$e \lt n\log n$.弧就是有向图的叫法。

• 稠密图：有较多的边或弧的图。

• 网： 边/弧带全的图。

• 邻接：有边/弧相连的两个顶点之间的关系，

  • 存在$(v_i, v_j)$,则称$v_i, v_j$为邻接点。圆括号表示不区分先后顺序。
  • 存在$<v_i, v_j>$，则称$v_i$邻接到$v_j$,而$v_j$邻接于$v_i$。尖括号表示有先后顺序。

• 关联（依附）：边、弧与顶点间的关系

  ​ 存在$(v_i, v_j)/<v_i, v_j>$,则称该边、弧关联与$v_i$和$v_j$。

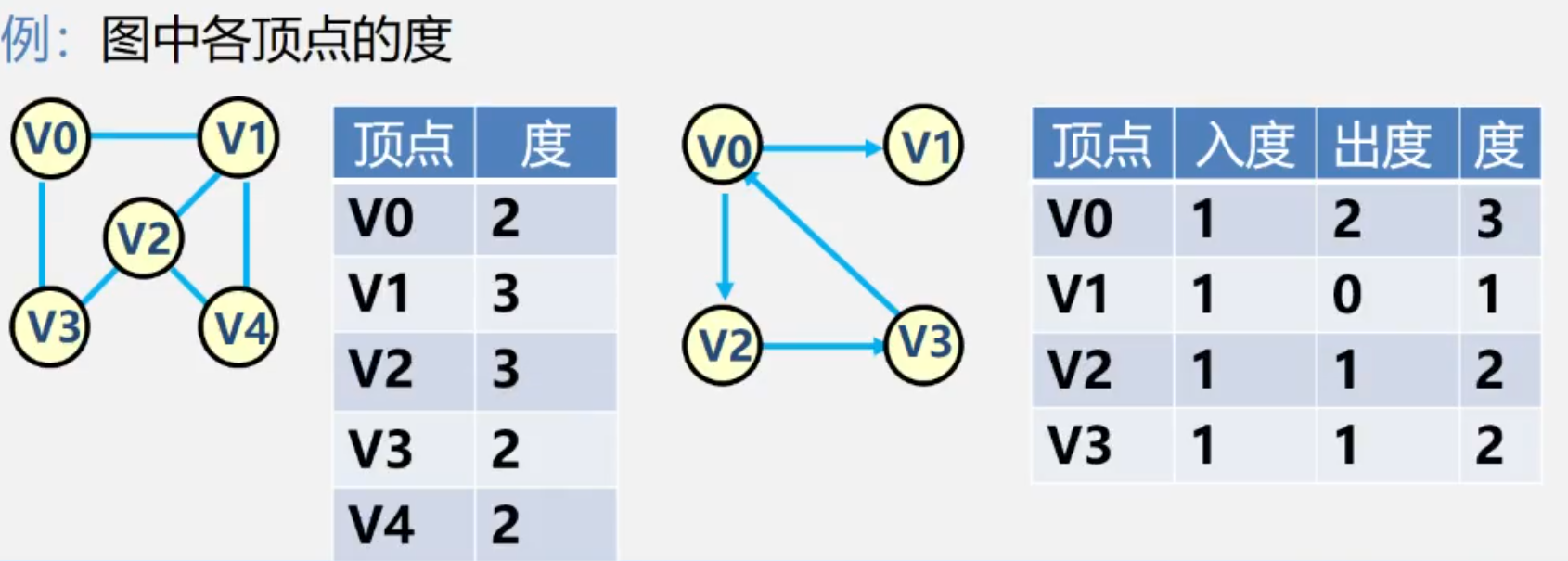
• 顶点的度：与该顶点相关联的边的数目，记为TD(v)。

  • 在有向图中，顶点的度等于该顶点的入度和出度之和。
  • 顶点v的入度是以v为终点的有向边的条数，记为ID(V)。
  • 顶点v的出度是以v为始点的有向边的条数，记为OD(V)。

  如下图例子所示，

  

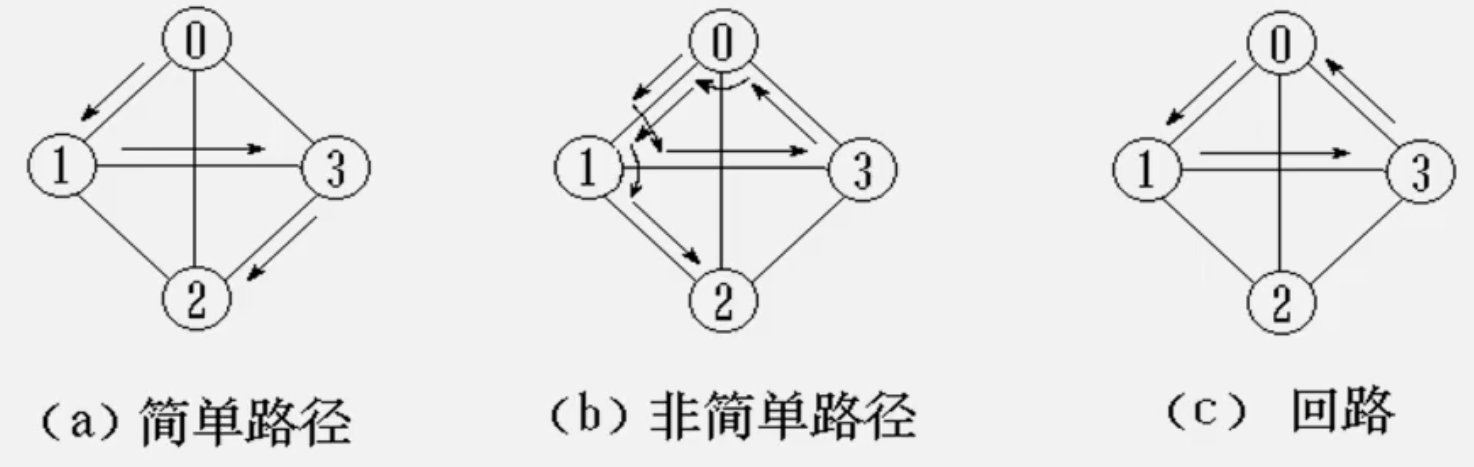
跟路径有关的定义：

1. 路径：接续的边构成的顶点序列。
2. 路径长度：路径上边或弧的数目/权值之和。
3. 回路(环)：第一个顶点和最后一个顶点相同路径。
4. 简单路径：除路径起点和终点可以相同外，其余顶点均不相同的路径。
5. 简单回路(简单环)：除路径起点和终点相同外，其余顶点均不相同的路径。

1. 连通图(强连通图)：在无/有向图$G=(V, {E})$中，若对任何两个顶点v、u都存在从v到u的路径，则称G是连通图。有向图满足这个条件就是强连通图。

1. 权：图中的边或弧所具有的相关数为权。表明一个顶点到另一个顶点的距离和耗费。

   ​ ——王卓 数据结构与算法

Inference

[1] CS224W-notes